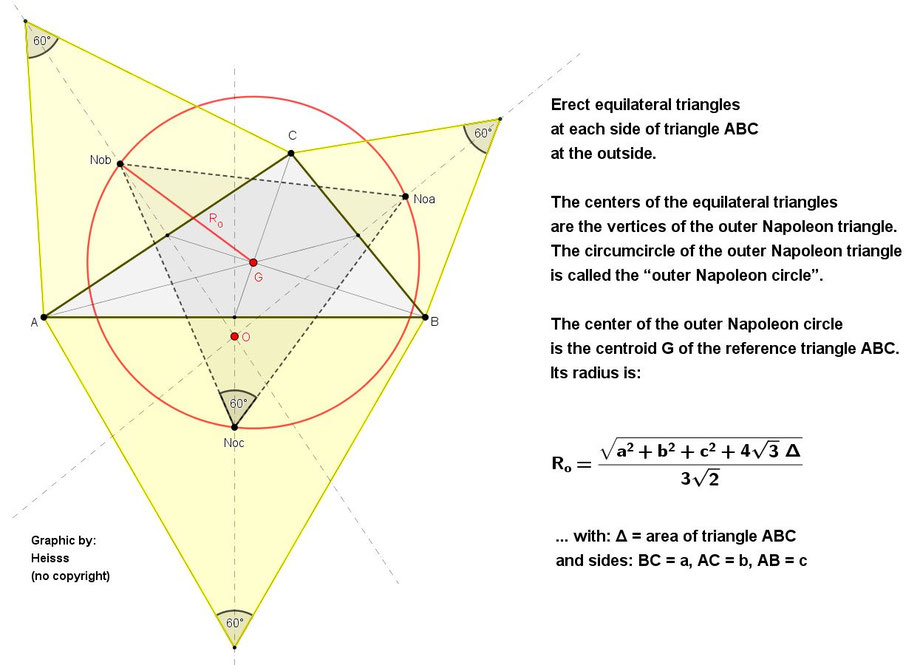
The Napoleon Triangles
... and Interessting Relationships
by
Markus Heisss
Würzburg, Bavaria
2018/2019/2020/2022/2024
Last Update: June 7, 2024
The copying of the following graphics is allowed, but without changes.
[To get a bigger picture, please click it with the cursor.]
Let's start with the outer Napoleon triangle :
And now the inner Napoleon triangle as graphic:
These triangles are named after the French Emperor Napoleon Bonaparte!
If he discovered these geometric relationships by himself is uncertain.
Further information you get from the internet under:
Connection of both Napoleon triangles
with the McCay circles and the circle of Apollonius:
Now both cases from above together, but first only at side AB:
Further information to "Circle of Apollonius": [here]
And finally the same at all three sides of the triangle:
**********************************
Postscript, March 24, 2022:
Relationship of the Napoleon circles
with the Steiner circumellipse:
Please note also the simple relationships between the radii of the Napoleon circles
and the semi-axes of the Steiner circumellipse!
**********************************
Postscript, May 31, 2024:
... And further discoveries to the Napoleon triangles:
Analogue with the inner Napoleon triangle:
And now a relationship with radical lines:
Again, analogue with the inner Napoleon triangle:
**********************************
Postscript, March 23, 2020:
... And further discoveries to the Napoleon triangles:
the Napoleon triangles and the Steiner circumellipse:
... and now triangles with the nine-point center:
**********************************